Optimal Planning Tutorial

Defining an optimal motion planning problem is almost exactly the same as defining a regular motion planning problem, with two main differences:

1. You need to specify an optimization objective to ompl::base::ProblemDefinition.
2. You need to use an optimizing planner for the actual motion planning.

Finding a shortest path

We'll demonstrate OMPL's optimal planning framework with an example. In this example, our robot is represented as a (x,y) coordinate on a square, where (0,0) is the square's bottom-left corner and (1,1) is the square's top-right corner. There is also an obstacle in this square that the robot cannot pass through; this obstacle is a circle of radius 0.25 centered at (0.5,0.5). To reflect this environment, we use a two-dimensional ompl::base::RealVectorStateSpace and define our state validity checker as follows:

// Our collision checker. For this demo, our robot's state space
// lies in [0,1]x[0,1], with a circular obstacle of radius 0.25
// centered at (0.5,0.5). Any states lying in this circular region are
// considered "in collision".
class ValidityChecker : public ob::StateValidityChecker
{
public:
    ValidityChecker(const ob::SpaceInformationPtr& si) :
        ob::StateValidityChecker(si) {}
 
    // Returns whether the given state's position overlaps the
    // circular obstacle
    bool isValid(const ob::State* state) const
    {
        return this->clearance(state) > 0.0;
    }
 
    // Returns the distance from the given state's position to the
    // boundary of the circular obstacle.
    double clearance(const ob::State* state) const
    {
        // We know we're working with a RealVectorStateSpace in this
        // example, so we downcast state into the specific type.
        const ob::RealVectorStateSpace::StateType* state2D =
            state->as<ob::RealVectorStateSpace::StateType>();
 
        // Extract the robot's (x,y) position from its state
        double x = state2D->values[0];
        double y = state2D->values[1];
 
        // Distance formula between two points, offset by the circle's
        // radius
        return sqrt((x-0.5)*(x-0.5) + (y-0.5)*(y-0.5)) - 0.25;
    }
};

In our planning code, we then define our state space, its bounds, and our start and goal states. In this example, the start state is at (0,0) and our goal state is (1,1) - i.e. the bottom-left and top-right corners, respectively. This code should be familiar if you've worked with regular motion planning in OMPL.

// Construct the robot state space in which we're planning. We're
// planning in [0,1]x[0,1], a subset of R^2.
ob::StateSpacePtr space(new ob::RealVectorStateSpace(2));
 
// Set the bounds of space to be in [0,1].
space->as<ob::RealVectorStateSpace>()->setBounds(0.0, 1.0);
 
// Construct a space information instance for this state space
ob::SpaceInformationPtr si(new ob::SpaceInformation(space));
 
// Set the object used to check which states in the space are valid
si->setStateValidityChecker(ob::StateValidityCheckerPtr(new ValidityChecker(si)));
 
si->setup();
 
// Set our robot's starting state to be the bottom-left corner of
// the environment, or (0,0).
ob::ScopedState<> start(space);
start->as<ob::RealVectorStateSpace::StateType>()->values[0] = 0.0;
start->as<ob::RealVectorStateSpace::StateType>()->values[1] = 0.0;
 
// Set our robot's goal state to be the top-right corner of the
// environment, or (1,1).
ob::ScopedState<> goal(space);
goal->as<ob::RealVectorStateSpace::StateType>()->values[0] = 1.0;
goal->as<ob::RealVectorStateSpace::StateType>()->values[1] = 1.0;
 
// Create a problem instance
ob::ProblemDefinitionPtr pdef(new ob::ProblemDefinition(si));
 
// Set the start and goal states
pdef->setStartAndGoalStates(start, goal);

Next, we want to define an ompl::base::OptimizationObjective for optimal planning. For now, we can specify an objective that corresponds to finding a shortest path between the start and goal states. We'll define another function that returns this particular objective:

// Returns a structure representing the optimization objective to use
// for optimal motion planning. This method returns an objective which
// attempts to minimize the length in configuration space of computed
// paths.
ob::OptimizationObjectivePtr getPathLengthObjective(const ob::SpaceInformationPtr& si)
{
    return ob::OptimizationObjectivePtr(new ob::PathLengthOptimizationObjective(si));
}

We can then set this as our objective in our planning code:

pdef->setOptimizationObjective(getPathLengthObjective(si));

Note: The optimizing planner we're about to use, ompl::geometric::RRTstar, actually defaults to optimizing for path length if no optimization objective is specified to the ompl::base::ProblemDefinition. This means that, in this case, the above statement isn't required. But if you want to optimize a metric other than path length, you have to manually specify it to the ompl::base::ProblemDefinition.

Next, we define our optimizing planner and attempt to solve the optimal planning problem:

// Construct our optimizing planner using the RRTstar algorithm.
ob::PlannerPtr optimizingPlanner(new og::RRTstar(si));
 
// Set the problem instance for our planner to solve
optimizingPlanner->setProblemDefinition(pdef);
optimizingPlanner->setup();
 
// attempt to solve the planning problem within one second of
// planning time
ob::PlannerStatus solved = optimizingPlanner->solve(1.0);

Here's an animation demonstrating the progress of the RRTstar planner on the problem we just defined:

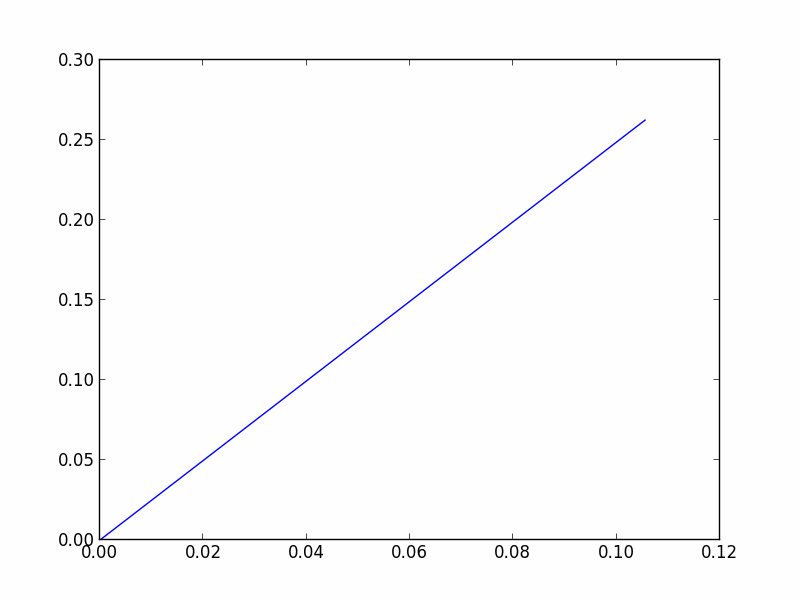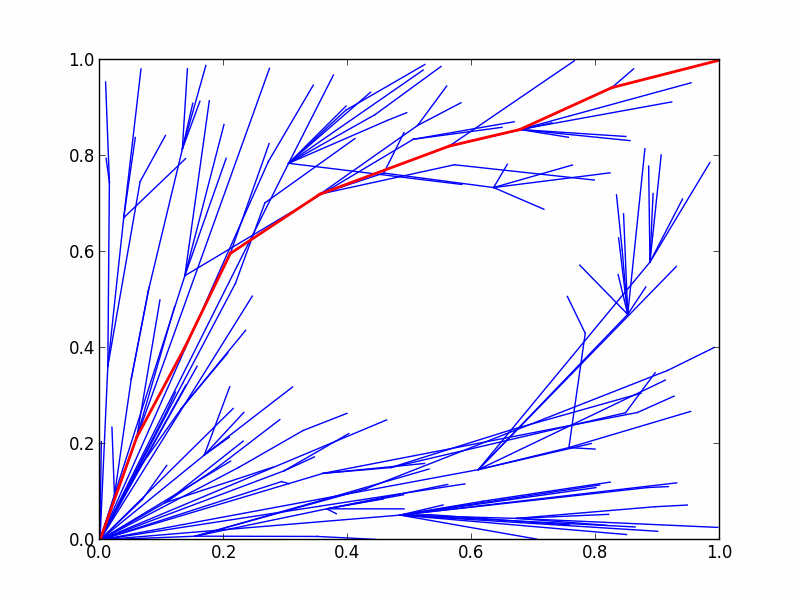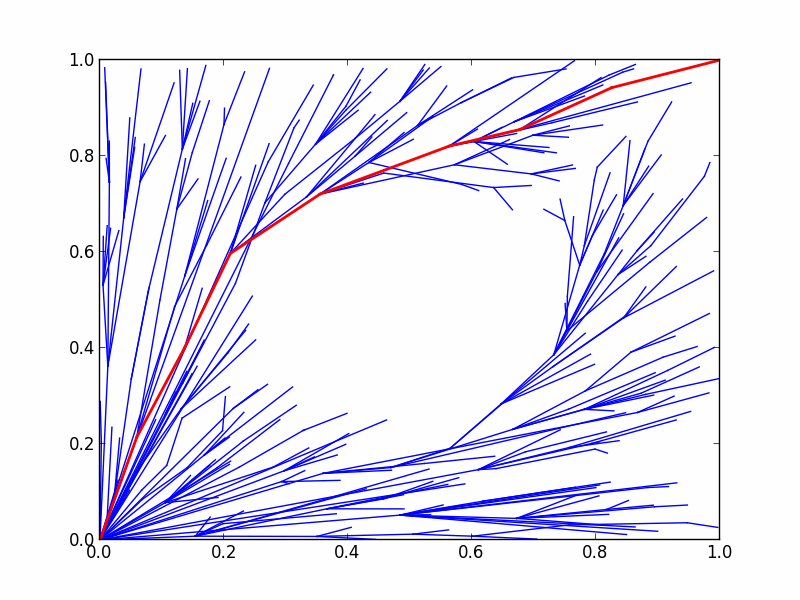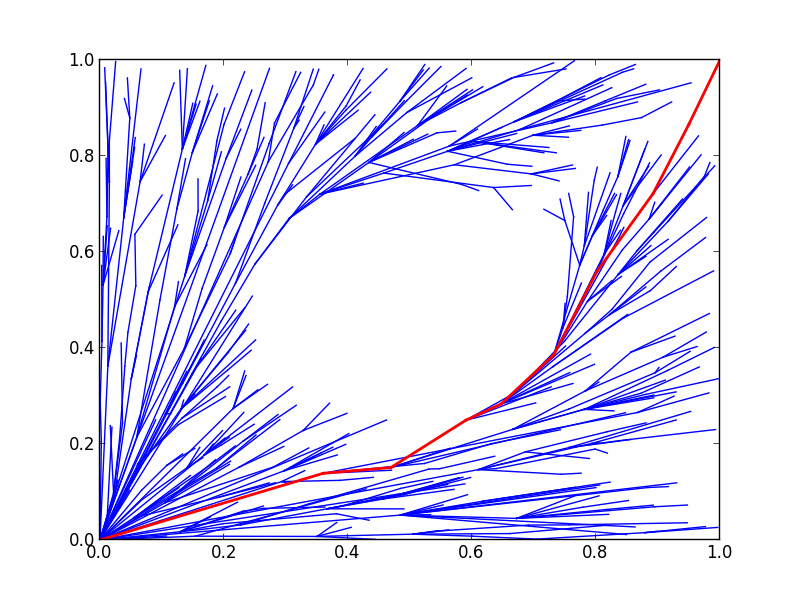
Note that when attempting to solve the planning problem, we specify a time limit of 1 second. In regular motion planning, the planner will stop as soon as a path between the start and goal states has been found - this can take far less than 1 second of planning. However, if you execute this example you'll notice that the planner always takes the full planning time of 1 second. This is because optimizing planners have a stricter stopping requirement than regular planners. Regular planners stop when they've found a path from start to goal; on the other hand, optimizing planners stop when they've found a path from start to goal that satisfies the optimization objective.

Specifying an optimality threshold

What does satisfying an optimization objective mean? This behaviour can be customized, but by default, it means finding a path that passes some quality threshold. For shortest path planning, it means finding a path that is shorter than some given length. You'll notice we never specified this threshold; the default behaviour for ompl::base::PathLengthOptimizationObjective is to set the threshold to 0.0 if a threshold wasn't specified. This means that the objective is only satisfied by paths of length less than 0.0, which means this objective will never be satisfied! Our reasoning for doing this is that, if you don't specify a threshold, we assume that you want the planner to return the best possible path it can find in the time limit. Therefore, setting a threshold of 0.0 means that the objective will never be satisfied, and guarantee that the planner runs all the way until the specified time limit and returns the best path it could find.

We can create an OptimizationObjective with a quality threshold of 1.51 by using the setCostThreshold method:

ob::OptimizationObjectivePtr getThresholdPathLengthObj(const ob::SpaceInformationPtr& si)
{
    ob::OptimizationObjectivePtr obj(new ob::PathLengthOptimizationObjective(si));
    obj->setCostThreshold(ob::Cost(1.51));
    return obj;
}

If you set this as the objective for the ompl::base::ProblemDefinition you'll find that the planner will terminate far more quickly, since it stops planning as soon as it has found a path shorter than the given threshold. Note that when calling ompl::base::OptimizationObjective::setCostThreshold, we wrap our threshold value in an ompl::base::Cost object. We'll talk more about the ompl::base::Cost object later, but for now you can think of them as a wrapper for double values that represent the cost of a path.