Multilevel Planning Framework

Table of Contents

• High-level introduction
• Why Use Multilevel Planning
• 100-dimensional Hypercube Benchmark
• Want to learn more?
  • Tutorials
  • Demos
  • Papers

When dealing with high-dimensional motion planning problems, we often cannot solve them directly because our algorithms either run out of memory or the runtime quickly blows up. To combat this curse of dimensionality, we can instead plan on different levels of abstractions. To plan on different levels of abstractions, we develop the multilevel planning framework. In this framework we use internally the language of Fiber Bundles to model abstractions as sequences of admissible lower-dimensional projections of the state space.

High-level introduction

Instead of planning on a single state space, we instead use a sequence of state spaces, which allows a planner to exploit those spaces to quickly find solutions. To use the multilevel planning framework, you only need to specify a sequence of ompl::base::SpaceInformationPtr together with corresponding ompl::base::StateValidityChecker functions. You can use any sequence and any validiy checker you like. However, if you want to be sure that the algorithm finds a solution, you need to make sure that those functions are admissible. Admissible here means that if there exists a valid solution on the original state space, and you project this solution onto a lower-dimensional space in your sequence, then this solution must be feasible. In practice, you can achieve admissibility by constraint relaxation operations, like shrinking obstacles, shrinking links, removing non-holonomic constraints, removing links, removing subsystems or removing robots (from a set of robots).

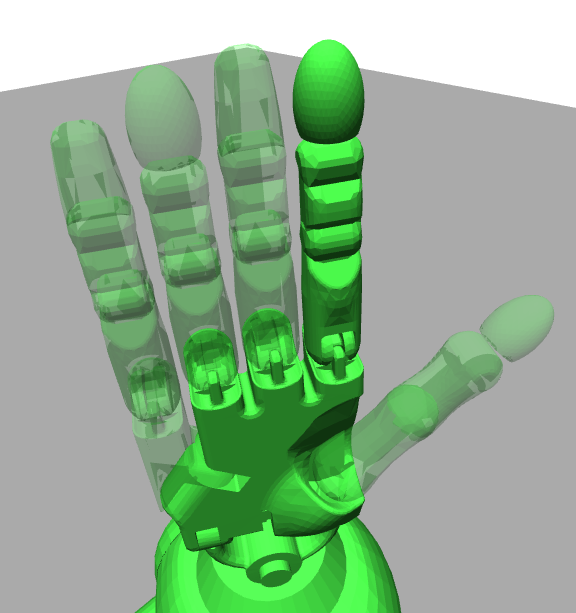
Some examples of admissible projections are shown in the Figure below. We show three examples. In the first example, we remove the arms of PR2 (which might be irrelevant when moving through long corridors). In the second example, we remove some fingers of the Shadow hand which might not be relevant for a particular grasp. In the third example, we nest an inscribed sphere in an airplane. While the airplane might have non-holonomic constraints, the sphere is holonomic. The validity checker in each case corresponds to checking collision of the lower-dimensional robot.

Why Use Multilevel Planning

• If you supply admissible projections, we can guarantee probabilistic completeness and asymptotical (near-) optimality
• It is more general than lower-dimensional projections
  • (1) We can handle a finite number of sequential projections instead of just one.
  • (2) We can project onto many manifold spaces instead of just euclidean space \(\mathbb{R}^N\).
  • (3) We can handle multiple robots and non-holonomic constraints
• It can be much faster compared to other planning algorithms (on the order of several magnitudes)

100-dimensional Hypercube Benchmark

To see how much faster multilevel planning can be, we provide a 100 dimensional hypercube demo, which you can run yourself using Multilevel HyperCube and Multilevel HyperCube Benchmark.

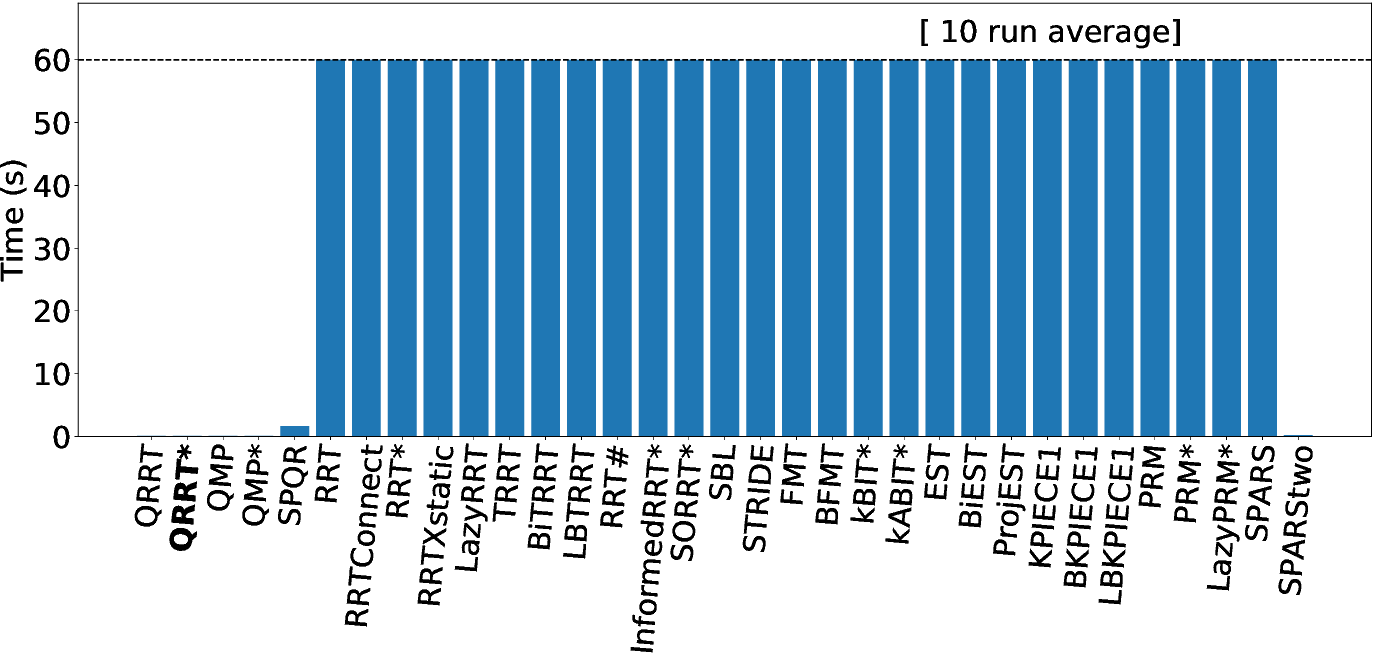
The abstractions in this scenario are \(99\) projections, where each projection removes a dimension from the problem and reduces the problem from an \(N\)-dimensional cube to an \(N-1\) dimensional cube. We compare several multilevel planning algorithms (QRRT, QRRT*, QMP, QMP*, SPQR) to all other algorithms currently implemented in the library (as of May 2020). Note that we had to remove planners ompl::geometric::SST and ompl::geometric::PDST due to memory issues. We observe that QRRT, QRRT*, QMP and QMP* all terminate in under one second (note that ompl::multilevel::SPQR and ompl::geometric::SPARStwo terminate while declaring the problem to be infeasible). Thus the multilevel planner significantly outperforms classical planner. Note that this problem is really hard, and classical planner can often only solve this problem with up to $25$ dimensions in reasonable time. It seems using multilevel planning is the only option to solve such challenging environments.