In this tutorial, we'll discuss how to implement your own customized optimization objectives for optimizing planners. We'll continue using the previous tutorial's example planning problem with the 2D robot and circular obstacle.
Specifying a new objective (part 1): path clearance
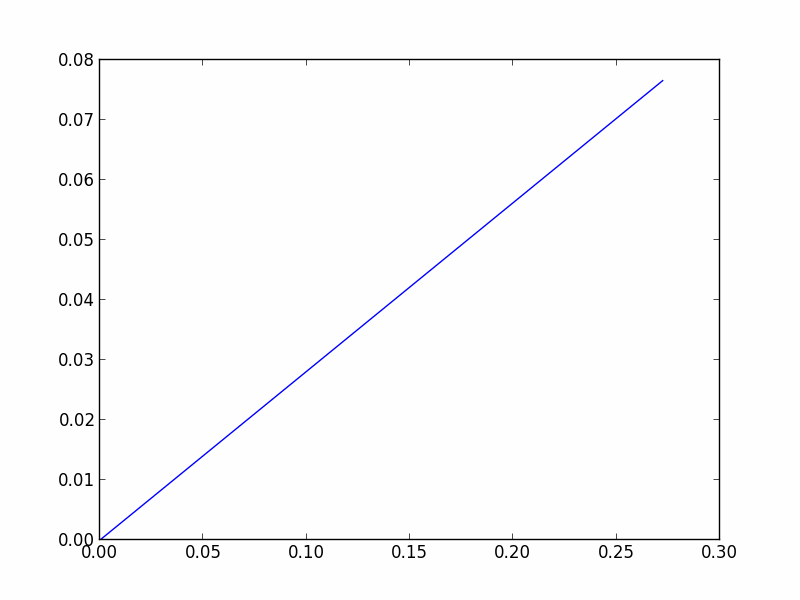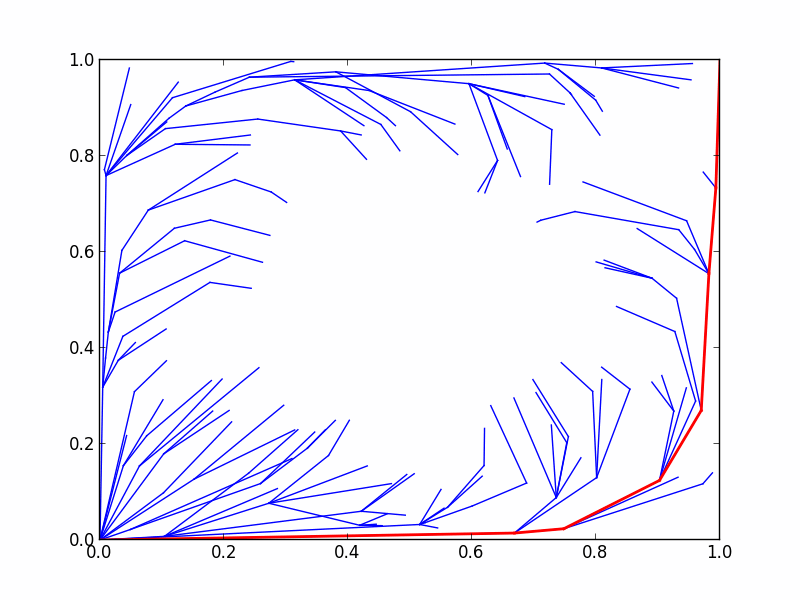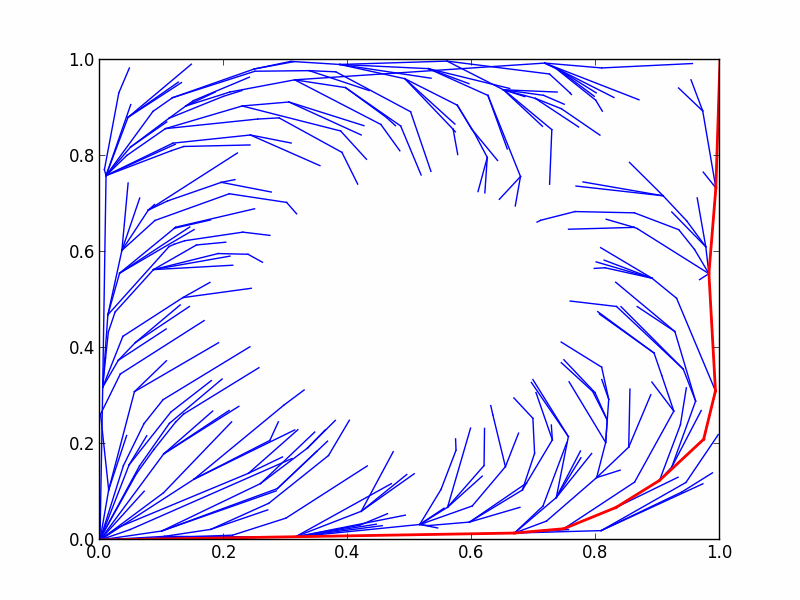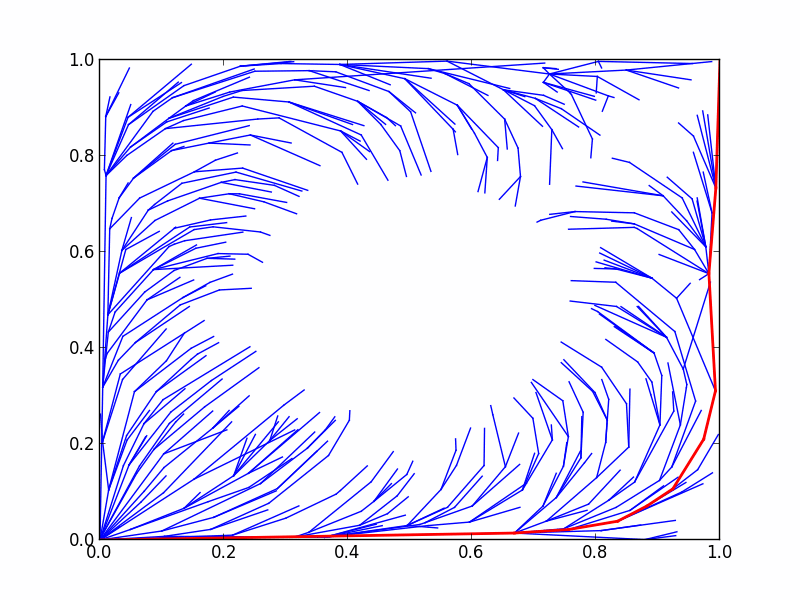
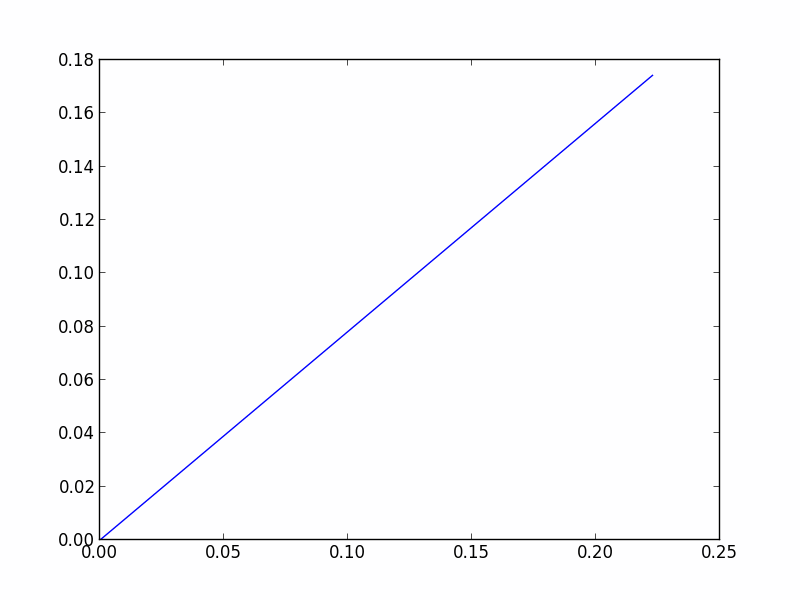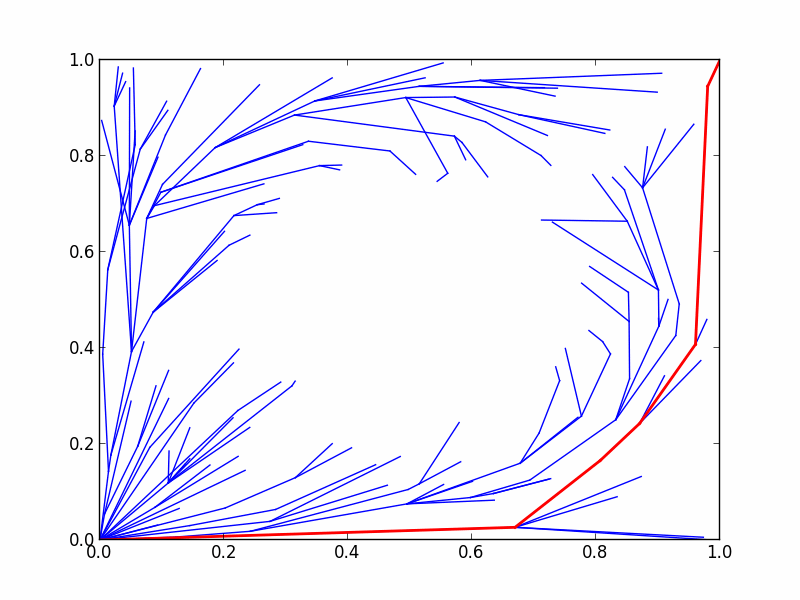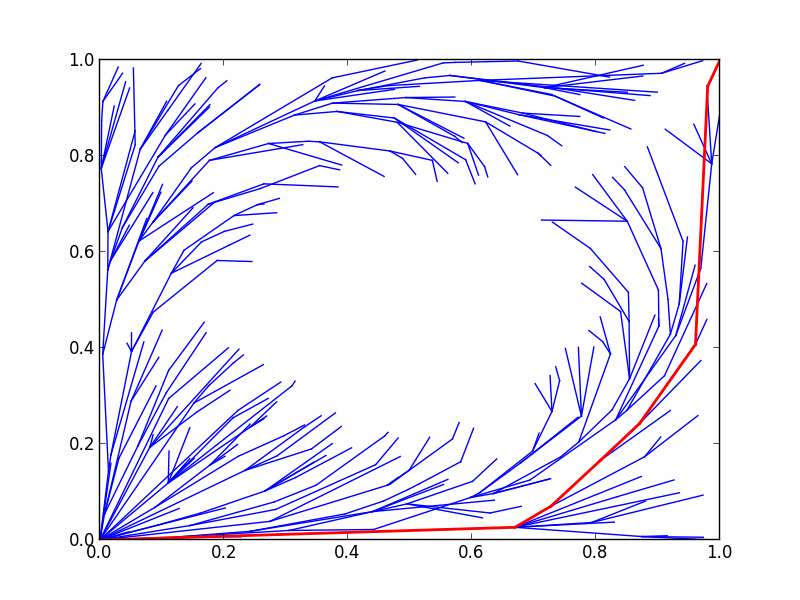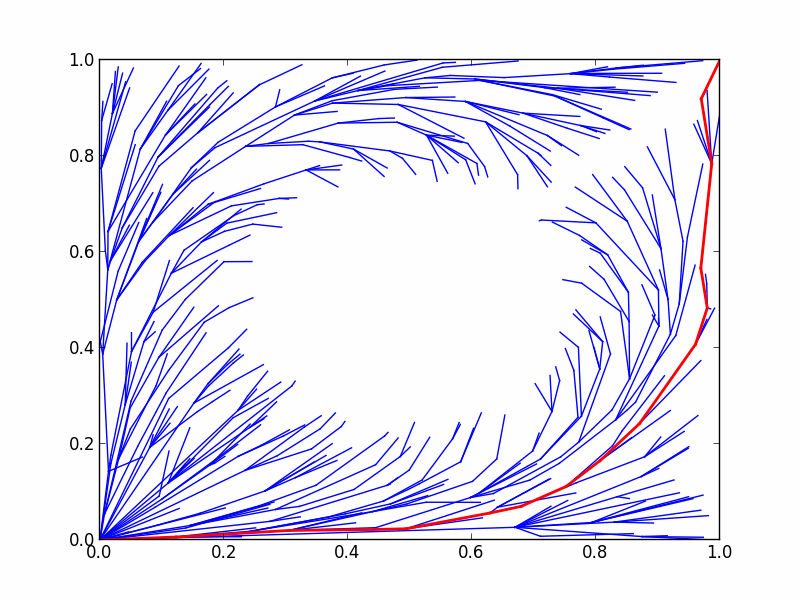
Previously, we considered optimal planning in terms of minimizing the length of the path found. However, this path tends to steer very close to obstacles, which can sometimes be unsafe. For safety reasons, let's define an objective which attempts to steer the robot away from obstacles. For this example, we chose to represent our metric of a path's clearance from obstacles as a summation of state costs along the path, where each state cost is a function of the state's clearance from obstacles.
In the above code fragment, you'll see that we've defined our path clearance objective as a subclass of ompl::base::StateCostIntegralObjective. This is because ompl::base::StateCostIntegralObjective represents objectives as summations of state costs, which is exactly what we require. Therefore, all we need to do to completely specify our path clearance objective is to inherit from ompl::base::StateCostIntegralObjective and specify our state cost function by overriding the ompl::base::OptimizationObjective::stateCost() method.
Now, let's talk about the counterintuitive implementation of ompl::base::OptimizationObjective::stateCost(). By default, optimization objectives seek to minimize path cost. For our path clearance objective, we want paths to maximize path clearance. Therefore, we want our state cost function to return smaller costs when states have greater clearance from obstacles. An easy way to do this is to simply define the state cost as the reciprocal of that state's clearance.
Lastly, notice that in ClearanceObjective's constructor we initialized the ompl::base::StateCostIntegralObjective with the additional argument true. This changes the behaviour of the objective to use motion cost interpolation when summing up state costs along the path. By default, ompl::base::StateCostIntegralObjective simply takes the individual states that make up a given path, and sums up those costs. However, this approach can result in an inaccurate estimation of the path cost if successive states on the path are far apart. If we enable motion cost interpolation the path cost computation will interpolate between distant states in order to get a more accurate approximation of the true path cost. This interpolation of states along a path is the same as the one used in ompl::base::DiscreteMotionValidator. Note that the increase in accuracy by using motion cost interpolation comes with a decrease in computational effiency due to more calls to ompl::base::OptimizationObjective::stateCost.
Here's an animation demonstrating the RRTstar algorithm's progress in planning under the above objective:
Multiobjective optimal planning
In some cases you might be interested in optimal planning under more than one objective. For instance, we might want to specify some balance between path clearance and path length. We can do this using the ompl::base::MultiOptimizationObjective class.
The above code fragment creates and optimization objective which attempts to optimize both path length and clearance. We begin by defining each of the individual objectives, and then we add them to a ompl::base::MultiOptimizationObjective object. This results in an optimization objective where path cost is equivalent to summing up each of the individual objectives' path costs. When we add objectives to ompl::base::MultiOptimizationObjective, we must also optionally specify each objective's weighting factor to signify how important it is in optimal planning. In the above example, we weigh the length with a factor of 10.0 and the clearance with a factor of 1.0 to try to balance more in favor of minimizing path length in planning. This objective results in a path which still maintains clearance from the circle, but not as much as before.
We also provide a more concise way to define multiple optimization objectives using operator overloading:
This function defines exactly the same optimization objective as the previous one, but uses fewer lines of code and represents the objective in a semantically rich form.
Here's an animation of the RRTstar algorithm's progress on this multiobjective problem:
Specifying a new objective (part 2): maximize minimum clearance
Now we'll implement an objective which will require a lot more tinkering with the rest of the methods in ompl::base::OptimizationObjective. This objective attemps to maximize the minimum path clearance; that is, the cost of a given path is only a function of the closest distance between the path and an obstacle. This objective has already been implemented for you as ompl::base::MaximizeMinClearanceObjective, but we'll walk you through your own implementation of it.
Here's the interface of our new objective, MaximizeMinClearance:
There're lots of methods here, but we're have some really cool functionality once we've finished! We'll go through the methods one by one.
Like in the previous objectives, we can reason about the cost of a path by reasoning about the costs of individual states. Let's define our state cost:
You'll notice that we didn't use the reciprocal of the clearance as before. This is because, in the previous case, we were constraining ourselves to considering optimal planning as a minimization of path cost (this was so that we could make use of the already-implemented functionality in ompl::base::StateCostIntegralObjective). However, we can turn the objective into a maximization of cost (and therefore a maximization of clearance) by overriding the ompl::base::OptimizationObjective::isCostBetterThan method:
Optimizing planners use this method to decide whether one path is better than another. It takes two cost values, c1 and c2, and returns true if c1 is considered a better cost than c2 by some threshold. The objects of type ompl::base::Cost are simply wrappers for double values which can be accessed with ompl::base::Cost::v; so, cost c1 is considered better than cost c2 if c1's value (path clearance) is greater than that of c2. We add the threshold ompl::magic::BETTER_PATH_COST_MARGIN to ensure numerical robustness in the optimizing planners. We recommend you use this threshold too if you override ompl::base::OptimizationObjective::isCostBetterThan.
- Note
- You might be wondering why we took the trouble of wrapping
doublevalues in a class to represent costs (instead of using atypedeffor instance). The reason why is type safety. Ifompl::base::Costwere simply atypedefofdouble, a user might accidentally use the<operator instead ofompl::base::OptimizationObjective::isCostBetterThan, which could cause some hard-to-find errors (this author knows from experience!). By using an object to represent costs, this mistake will be caught by the compiler.
In a way, maximizing minimum clearance can be formulated similarly to the previous objectives. Your path is a sequence of states, and the path cost can still be represented as a special combination of the state costs along the path; while in the previous cases, this combination was addition, in the case of minimum clearance, the combination is the min function. We can therefore specify this functionality for our objective by overriding the ompl::base::OptimizationObjective::combineCosts method:
The implementation of this method in the base class ompl::base::OptimizationObjective simply sums the two costs given as arguments. In our case, we return the minimum of the two costs, which is equivalent to returning the minimum clearance of the two. If we accumulate the cost of a path using this operation instead of addition, we'll get the minimum clearance of the entire path as desired.
Next, we need to specify how to compute the cost of a motion defined by the two endpoints of the motion. Technically, the cost of the motion comes from the minimum clearance over the entire continuum of states along that motion. In most real-world motion planning problems this is very difficult to compute, so we have to settle for an approximation. One approximation is to simply take the the minimum of the clearances of the two endpoints; we'll implement this approximation as an example for simplicity, but it's a much better idea to sample some interpolating states along the motion for more accuracy, as is done in ompl::base::MinimaxObjective::motionCost. Here's how we implement the two-endpoint approximation of motion cost:
You'll notice that this simple approximation of motion cost can be implemented using our already-defined combineCost and stateCost methods.
Many optimizing planners count on their objectives having certain cost values which have special properties. One common cost value is the identity cost. This is a cost value c0 which, when combined with any other cost value c1 using combineCost, always returns the value c1. For example, when combineCost is simple addition, the identity cost is 0. We can specify an objective's identity cost by overriding the ompl::base::OptimizationObjective::identityCost method; but what is the identity cost of our minimum cost objective? It's a cost that, when combined with another cost with the min function, always returns the other cost. This means that the identity cost must be greater than every other cost - in other words, infinity!
We define the identity cost of our minimum path clearance objective to be infinity. Because we're working with costs, we wrap the double value of infinity in a Cost object.
Another cost value commonly used in optimizing planners is the infinite cost. This is a cost which is worse than all other cost values; in other words, it's a value c_i for which isCostBetterThan(c_i, c) is false for all values of c. In the case of our minimum clearance objective, we can use the value of negative infinity to fulfill this role. We specify this by overriding the ompl::base::OptimizationObjective::infiniteCost method:
Our objective is now ready to be used for planning! In the previous tutorial, we used the ompl::geometric::RRTstar planner for optimal planning; you may find you get nicer results if you use the ompl::geometric::PRMstar planner for this problem. You can use it with the following code (after defining your planning problem and optimization objective):
Cost Heuristics
Some optimizing motion planners such as ompl::geometric::PRMstar can plan more efficiently if you provide them with cost heuristics. A heuristic is a function which quickly computes an approximation of some value. There are two kinds of cost heuristics defined in OMPL:
- Motion cost heuristics approximate the cost of the optimal path between two given states
- Cost-to-go heuristics approximate the cost of the optimal path between a given state and the goal
Specifying cost heuristics for an optimization objective can speed up the planning process by providing optimizing planners a fast way to get more information about a planning problem.
Admissible heuristics
In order for optimizing planners to most effectively use a cost heuristic, the cost heuristic must have an important property called admissibility. An admissible cost heuristic always underestimates the cost of a path. That is, if the true optimal cost of a path is c_o, an admissible heuristic never returns a cost c_h such that isCostBetterThan(c_o, c_h) is true.
Motion cost heuristics
Let's consider what an admissible motion cost heuristic would look like when planning to minimize path length for a 2D point robot. The shortest possible path between two points is a straight line. We can quickly compute the length of this path with ompl::base::SpaceInformation::distance. Note that the true optimal path between the two points might be longer because of obstacles in the environment; however, we can at least guarantee that the value returned by ompl::base::SpaceInformation::distance is never longer than length of the truly optimal path. Therefore, ompl::base::SpaceInformation::distance is an admissible heuristic! In fact, this is precisely how we implemented ompl::base::PathLengthOptimizationObjective::motionCostHeuristic:
Note that the default implementation of ompl::base::OptimizationObjective::motionCostHeuristic simply returns the objective's identity cost, which is guaranteed to be an admissible heuristic for most objectives. However, this isn't a very accurate approximation of motion cost, and motion planners typically experience greater speedups when heuristics more accurately approximate motion cost. Therefore, if your optimal planning problem allows for a more accurate and quick-to-compute admissible heuristic, we recommend you provide one by implementing ompl::base::OptimizationObjective::motionCostHeuristic.
Cost-to-go heuristics
Cost-to-go heuristics can provide even more information to a planner by quickly approximating the optimal path cost between a given state and the goal. However, cost-to-go heuristics must be specified differently from motion cost heuristics: instead of overriding a method as with motion cost heuristics, we need to supply a function pointer to the objective using ompl::base::OptimizationObjective::setCostToGoHeuristic. This is necessary because one optimization objective might be used with many different types of goals, and heuristic calculations can differ depending on the goal type. As with motion cost heuristics, an optimizing planner is most effective when the provided cost-to-go heuristic is admissible and is an adequate approximation of the true optimal path cost between a given state and the goal.
Let's look at how we can use a cost-to-go heuristic in our 2D point robot problem. Assume we're interested in minimizing path length. In this example, the goal is defined as all states within a given tolerance distance of a specified goal state. Therefore, a shortest possible path between a given state and the goal is equal to the straight-line distance between the state and the goal state minus the goal tolerance. This is an admissible heuristic on the cost-to-go distance, and is already defined for you as ompl::base::goalRegionCostToGo:
This cost-to-go heuristic function can handle any goal of type ompl::base::GoalRegion, because these goals define a notion of goal distance in the form of ompl::base::GoalRegion::distanceGoal. We have to subtract the goal threshold in the cost-to-go calculation because a shortest path to the goal from a given state isn't to the center of the goal region, but to the boundary. Lastly, we use std::max to ensure we don't return a negative cost. We can create a path length objective that uses this cost-to-go heuristic with the following function:
It's extremely important to note that the ompl::base::goalRegionCostToGo heuristic is only valid for your planning problem if ompl::base::GoalRegion::distanceGoal is an admissible heuristic on the optimal path cost from a state to your goal region. For instance, if you're planning with ompl::base::MaximizeMinClearanceObjective to maximize minimum path clearance, the ompl::base::goalRegionCostToGo function would not be a suitable cost-to-go heuristic because ompl::base::GoalRegion::distanceGoal has no correlation with path clearance.