From differential equations to planning in one function

When planning for a physical robot, the motion of the system is constrained due to those pesky “laws of physics.” If you drive your car to the grocery store, you cannot directly control the position of the car or even how fast it moves down the street. Terrifying! You can only control the rate at which the velocity changes (acceleration) and the direction the car is steering toward. Furthermore, the acceleration of our cars is bounded; we cannot stop immediately or achieve a particular speed instantly. This makes the car a second-order system. We can directly control the acceleration, but the velocity and position are the result of the changes in acceleration and steering angle over time. The same scenario applies to physical robots: a typical system cannot be explicitly controlled. Instead, we apply a series of inputs (like pressing the gas or the brake in a car) to control motors and other actuators to execute a motion plan. Mathematically we can describe the motion of a robot as a set of ordinary differential equations which depend on an input control and time. The exact state of a robot can then be computed by integrating the equations given the control input and duration to apply that input.

OMPL’s StatePropagator concept can be used to incorporate integration of the differential equations for the system, but the user is tasked with implementing the ODE, integrating the equations and updating the state for the system, as in the rigid body planning with integration and controls demo. This task is simplified in OMPL v0.10 with the addition of the ODESolver class, which takes care of numerical integration and state updates. All the user has to do is provide the ODE definition in a single function:

void ODE(const ODESolver::StateType &q, const Control *c, ODESolver::StateType &qdot)
    /* Insert code here */
}

This method takes the input state q and a control c, and computes the change in the value of q, storing the differential into qdot. The ODESolver wraps around the open-source ODEInt library, which provides methods for high-order numerical integration. Gone are the days of worrying about the numerical instability and potential large error of quick and dirty Euler integration. A StatePropagator object can be extracted from the ODESolver class which encapsulates the entire integration and update process.

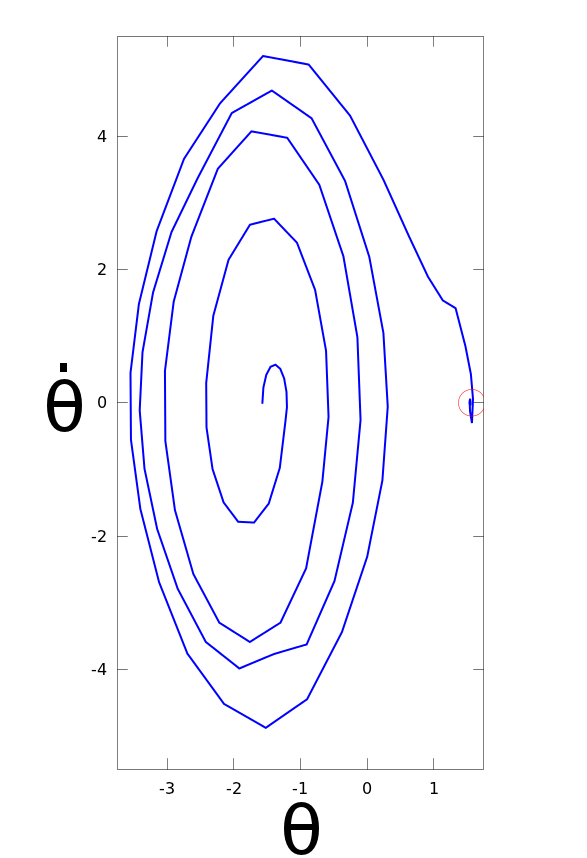
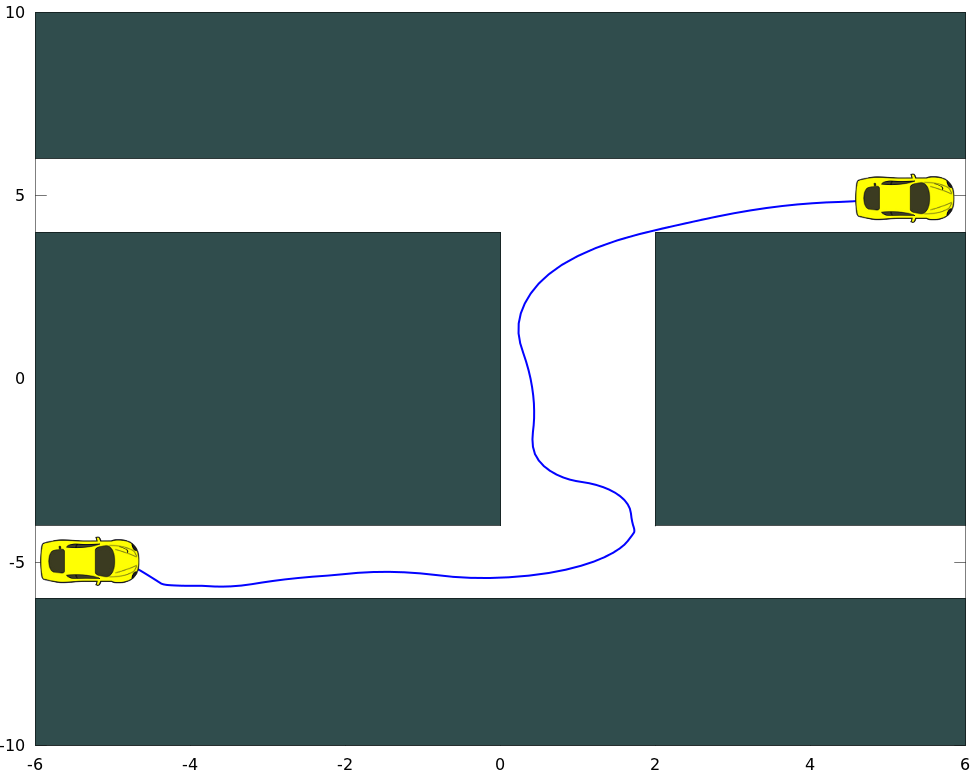
A tutorial has been created to show how to use OMPL’s ODESolver class in further detail. A new demo is also bundled in OMPL v0.10, rigid body planning with ODESolver and controls, which shows a comparison with the “old” way of doing things and how the ODESolver simplifies this process. The ODEInt library is bundled with OMPL, so there is no extra dependency to install, and by using the ODESolver class you’ll be planning for your system in no time! Below are plots of actual paths computed using the ODESolver for an inverted pendulum and a second-order car: